Asymptotic methods allowing considering a large set of surface roughness scales have been developed. Three parameters are used to characterize the surface:

• The roughness depends on the ratio from the surface RMS to the wavelength,
• The slope is defined as the ratio of the roughness to the autocorrelation distance of the irregularities,
• The autocorrelation function

Three kinds of models have been developed allowing considering a large number of cases:

• Small roughness : the small slope approximation, augmented by the non local small slope approximation
• Average and high roughness : the algorithm is based on the Kirchhoff approximation
• Very strong roughness : the algorithm uses the second order Kirchhoff approximation

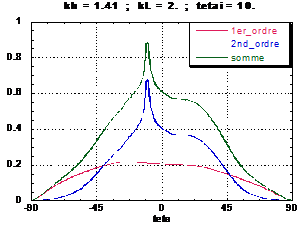
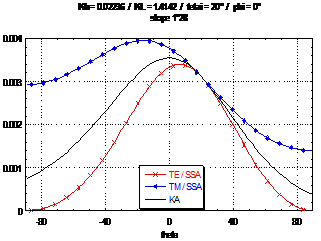
Scattering function Kirchhoff  approximation1st and 2nd ordre	Scattering function Small Slope Approximation technique (SSA) compared to the Kirchhoff approximation

References

(full texts available in the publications section)

Y. Beniguel, G. Berginc, "Une revue des techniques utilisees pour le calcul de la diffraction par les surfaces rugueuses aleatoires", Journees d'etudes sur la propagation electromagnetique dans l'atmosphere : du decametrique a l'angstrom, Rennes, 2002.

G. Berginc, Y. Beniguel, B. Chevalier, "Small slope approximation method : Higher order contributions for scattering from conducting 3D surfaces", SPIE99 Proceedings, Denver, 1999